Mucha gente llama a los LLM “máquinas inteligentes”, lo que lleva naturalmente a preguntarse: ¿realmente entienden o reconocen patrones simples?
Estudiemos esta pregunta usando un test muy sencillo.
Un test simple: completar patrones
Una forma directa de evaluar si un modelo reconoce un patrón es pedirle que lo complete. Le das una secuencia que sigue una cierta lógica, y le pides predecir el siguiente elemento. Esto es básicamente lo que hacen los LLMs: predicción del próximo token (Next Token Prediction, NTP). Toda su etapa de entrenamiento gira en torno a eso.
Entonces, para probar esto, necesitamos una secuencia.
Secuencias simples: fichas rojas y azules
Imaginemos una tabla (como un tablero de ajedrez) con fichas rojas y azules. Una secuencia sería simplemente ir agregando fichas en fila. Si se acaba la fila, continuamos con la siguiente. La secuencia más simple que se te puede ocurrir es: todas las fichas del mismo color. Por ejemplo, 9 fichas rojas seguidas.
Si después de ver 9 fichas rojas seguidas, te preguntan cuál debería venir después, probablemente digas: otra roja. Si ves 99 rojas, tu confianza en que viene otra roja crece aún más. Esto nos dice que predecir el siguiente término de una secuencia tiene más sentido cuando estas no son demasiado cortas. Y de hecho, con suficiente largo de secuencia los LLMs sí logran aprender este tipo de patrón (puedes probarlo tú mismo con el modelo que prefieras).
Introduciendo otra secuencia: rojo-azul-rojo-azul-rojo...
Ahora agreguemos una secuencia distinta: alternancia entre rojo y azul. Algo como: rojo, azul, rojo, azul, etc. A diferencia de la secuencia toda roja, esta tiene la mitad de sus fichas azules.
Podemos hablar aquí de una "distancia" entre secuencias. Por ejemplo:
- La secuencia toda roja tiene 0 fichas azules.
- La alternada rojo-azul tiene 50% azules.
Podemos decir entonces que estas dos secuencias están a “distancia” 0.5, sin importar su largo. Eso las hace claramente distinguibles, y los LLMs también pueden aprender ambas sin confusión.
Desafío: construir un modelo capaz de generar ambas secuencias
¿Puedes construir un modelo tipo LLM (un Transformer decoder-only de una sola capa) que sea capaz de generar, ficha por ficha, ambas de las siguientes secuencias?
- La secuencia constante: todas las fichas rojas.
- La secuencia alternante: rojo, azul, rojo, azul …
Hint: Imagina que el vocabulario del modelo contiene solo dos tokens: “0” representa una ficha roja, y “1” representa una ficha azul. Piensa que el LLM opera como un clasificador binario autorregresivo (token a token): a partir del prefijo observado, predice si el próximo token debe ser 0 o 1. Tu objetivo es encontrar una configuración de pesos para una arquitectura Transformer estándar (una sola capa, decoder-only, con atención y MLP), tal que:
Caso (1): Si el modelo recibe un prefijo de puros 0s (por ejemplo, 000000), debe predecir otro 0, es decir, retornar un escalar negativo (si asumimos una proyección final con “signo” para clasificar).
Caso (2): Si recibe un prefijo alternante como 010101..., debe predecir el próximo token de acuerdo al patrón:
- Si el último token fue 0, debe predecir un 1 (es decir, salida positiva).
- Si el último token fue 1, debe predecir un 0 (salida negativa).
Mándanos tus respuestas a cartas@fintual.com
¿Qué pasa con secuencias casi iguales?
Aquí viene lo interesante. ¿Qué pasa si tomamos la secuencia con 199 fichas todas rojas y le metemos una sola ficha azul en alguna parte (menos al final)? Esa nueva secuencia es 198 rojas y 1 azul, por ejemplo. Eso es un cambio pequeñísimo: aproximadamente solo un 0.5% de diferencia.
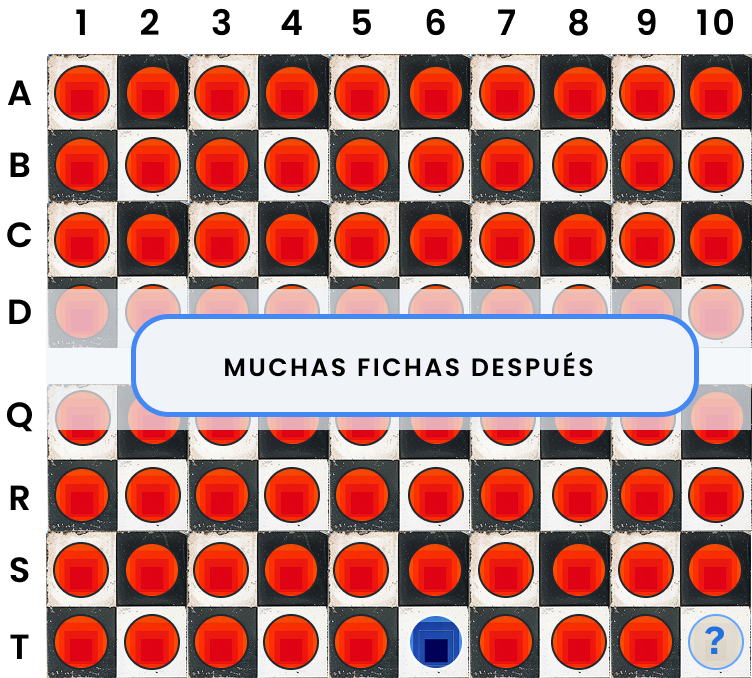
¿El LLM debería cambiar su predicción solo por eso? Probablemente no. Si interpretamos esa ficha azul como un "ruido", el modelo debería seguir prediciendo otra ficha roja.
Esto se relaciona con una propiedad matemática muy importante: continuidad. En palabras simples, si el input cambia muy poquito, el output también debería cambiar muy poquito. Los LLMs estándar tienen esta propiedad: son continuos. Y eso es bueno… hasta que deja de serlo.
Cuando la continuidad se convierte en un problema
Ahora pensemos en una secuencia más elaborada, pero que sigue pareciéndose a la toda-roja:
Imagina esta secuencia: azul - 2 rojas - azul- 4 rojas - azul- 6 rojas - azul - 8 rojas - ...
Aquí, los bloques de rojas van creciendo de a 2. Esto sigue una estructura: la posición de las fichas azules aparece en lugares que corresponden a cuadrados perfectos (1, 4, 9, 16…). O si quieres, el tamaño de cada bloque de rojas codifica los números pares.
El detalle clave: a medida que la secuencia crece, la proporción de fichas azules baja mucho. Con 40.000 fichas, quizás solo hay 200 azules (¡eso es un 0.005 de proporción!).
Desde el punto de vista del LLM, esta secuencia se ve muy parecida a la toda-roja. ¿Qué va a pasar? Por continuidad, el modelo probablemente no logre distinguirla, y falle en predecir correctamente las fichas azules donde debería. Aunque tenga una estructura lógica muy clara, el modelo la ignora por ser “casi igual” a otra que ya aprendió.
El dilema: aprender una implica no poder aprender otras
Esto nos lleva a un fenómeno más profundo: si el modelo aprende con confianza una secuencia, no puede aprender otras que están demasiado cerca. Por ejemplo, si un modelo aprende la secuencia toda-roja y se vuelve muy confiado en predecir rojas siempre, va a fallar con secuencias similares pero con estructura interna (como la de los cuadrados perfectos). En otras palabras: si el modelo es continuo y aprende con certeza una secuencia, puede perder sensibilidad a muchas otras secuencias “cercanas”.
Una reflexión final
Este problema es más común de lo que parece. Hay tareas donde los detalles sutiles importan mucho: por ejemplo, verificar si un código Python tiene un error de sintaxis. Un solo carácter extra o mal puesto puede hacer que el código no funcione, y un modelo continuo tal vez no note ese pequeño cambio.
Entonces, por más que los LLMs sean buenísimos en muchas tareas, tienen límites estructurales. Uno de esos límites es que la continuidad (una propiedad útil para evitar respuestas locas con entradas parecidas) también los hace ciegos a ciertos patrones delicados.
