La clave está en el color: es importante notar que cada dominó cubrirá siempre dos casillas adyacentes de distinto color. El tablero completo, por su parte, tiene 32 escaques de cada tono. No obstante, las casillas mutiladas por Beatriz pertenecían a la misma diagonal; por ende, comparten no solamente el dolor, sino el color. Tras el corte, se produce entonces una asimetría: quedan 30 casillas de un color y 32 del otro. Y considerando que cada dominó cubrirá una casilla de cada color, este desequilibrio convierte el recubrimiento en una tarea imposible para Ana.
Para la continuación, basta con generalizar el argumento anterior: eliminar dos casillas del mismo color —sean esquinas o no— provoca el mismo desbalance, de modo que ningún tapizado con dominós funcionará. Ahora bien, si los escaques son heterocromáticos, la situación se vuelve más interesante. Existen distintas demostraciones; la que aprendí dice más o menos así:
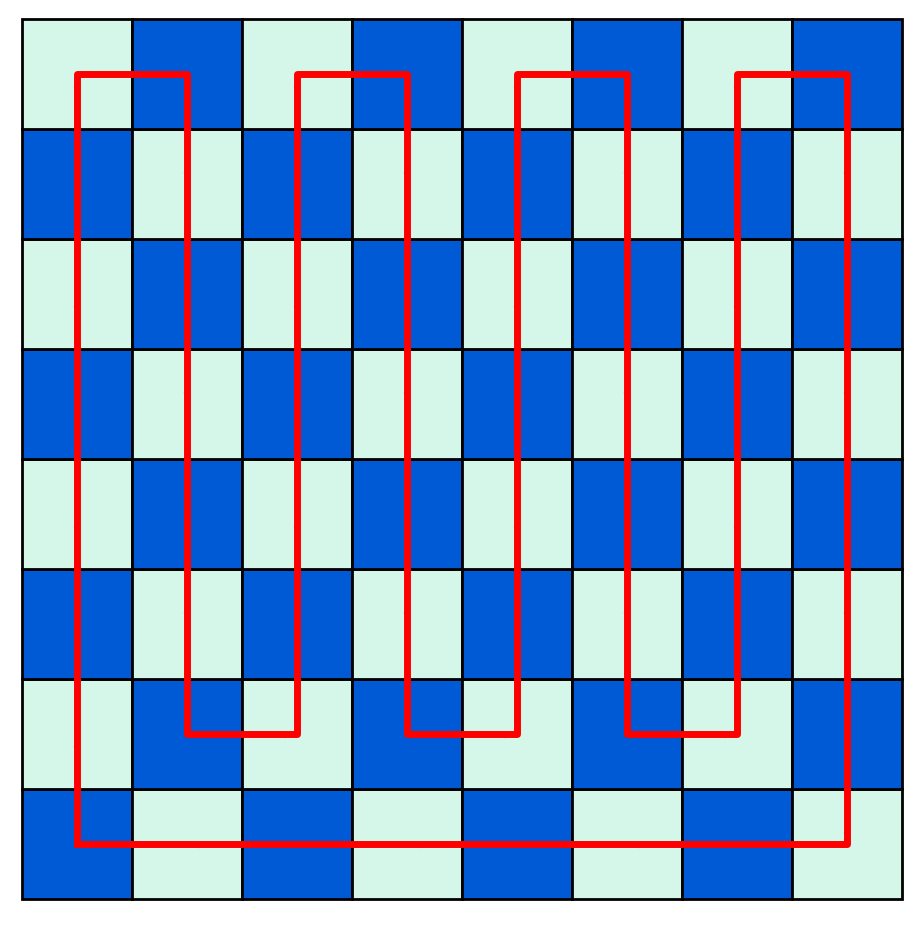
Tracemos un camino serpentino que recorre adyacentemente, una a una, las 64 casillas para, finalmente, volver al punto de partida. Hay varias formas de lograr esto; una de ellas puede observarse en el diagrama. [En matemática, esto corresponde a un ciclo hamiltoniano.]
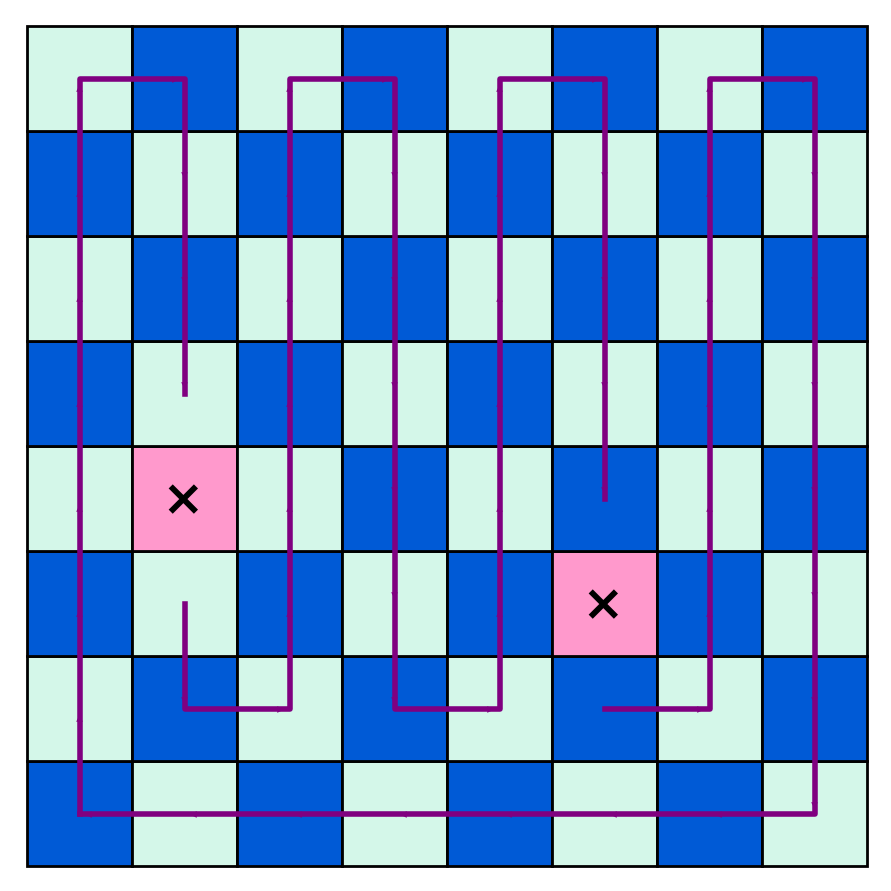
Al extraer dos casillas cualesquiera de distinto color, este camino se cortará inevitablemente en uno o dos tramos, cada uno de longitud par. Debido a esta condición, esto permitirá el recubrimiento de forma evidente.
Finalmente, hemos llegado a la conclusión: es posible cubrir el tablero mutilado con dominós si y sólo si los escaques eliminados tienen colores opuestos. Y todo esto… en exactamente 256 palabras.
Las mejores respuestas
Recibimos varias respuestas correctas, pero hubo una (enviada por Martín M) que destacó porque, matemáticamente hablando, fue la más detallada de todas. Está bien fundamentada: desarrolla el razonamiento paso a paso, explica cómo se construyen los rectángulos (considerando casos borde) y luego detalla cómo se rellenan las franjas periféricas. Además, el conjunto de diagramas es un buen acompañamiento en la explicación. Es un enfoque diferente para llegar a la misma solución. Si quieres verla, haz clic acá.
Por último, queremos ofrecerle una mención honrosa a Samuel G, quien partió de la ilustración del primer desafío de ajedrez que planteó Héctor Pastén y creó una variación —presumiblemente con IA— que aporta una hilarante y evidente continuidad a la historia entre Ana y Beatriz.
Por cierto, si te sobran tres minutos y prefieres una explicación audiovisual, te sugiero echarle un vistazo a este video publicado en The Guardian por Alex Bellos. Está en inglés, eso sí.
La primera vez que escuché sobre este desafío —hoy conocido como El problema del tablero de ajedrez mutilado— fue en este video de ChessNetwork, publicado en 2015. No obstante, su historia se remonta a 1946, cuando el filósofo y matemático Max Black lo propuso en su libro Critical Thinking. Luego, fue popularizado en la década de 1950 por distintos matemáticos; entre ellos, Martin Gardner quien, en 1957, lo convirtió en un clásico al comentarlo en su columna Mathematical Games del Scientific American. Y claro está, el 2025 en el Fintualist.