Si la renta fija es fija, ¿por qué entonces ese tipo de activos igual suben y bajan de precio? Creo que esto fue lo que más me costó entender de mis clases de finanzas.
Existen 2 principales tipos de activos: renta fija y renta variable (aquí te explicamos las diferencias). Y como decíamos al comienzo, la renta fija tiene algo que no es tan intuitivo, y que ahora te lo vamos a explicar.
Los activos de renta fija
Al invertir en renta fija, estás prestándole plata a alguien. Tomas un depósito a plazo en un banco, y el banco se está endeudando contigo: tú le prestas $1.000 al banco esperando que el banco te vaya a devolver, digamos, $1.010.
Un depósito a plazo es un tipo de activo de renta fija, y más extensiblemente, los activos de renta fija se llaman bonos. No son muy distintos conceptualmente a un depósito a plazo. Una determinada empresa o institución dice “necesito plata prestada y estoy dispuesto a pagar X en tanto tiempo más. Quién me presta?”.
Algunas peculiaridades que pueden tener los bonos están principalmente en la forma en la que pagan. En lugar de pagar todo al final del préstamo, es común que se hagan distintos pagos a lo largo del tiempo, a los que se les llama cupones.
En cualquier caso, cuando compras un bono, estás seguro de la cantidad que vas a recibir. La excepción a esto es que quien te debe la plata no te pueda pagar, eso se llama riesgo de crédito, y es uno de los riesgos que existe al invertir en instrumentos de renta fija.
Pero dejemos ese escenario a un lado, pongámonos en el caso feliz. Compras un bono a $10.000, que te dice que te hará un único pago al cabo de 10 años, a una tasa anual de 5%. Entonces, lo que te van a pagar (estamos asumiendo que te lo pagarán) es $16.289:
$$10.000 \cdot \left(1 + {0,05}\right)^{10} $$
Si el día que lo compras tu bono vale $10.000, y en 10 años más te pagarán $16.289, es esperable que vaya cambiando de precio:, ¿por qué querrías vender tu bono a $10.000 cuando quede apenas un día para que te paguen el total? Todo ese tiempo que vas teniendo tu bono tiene un valor, aunque aún no te lo hayan pagado. Eso se llama devengo.
¿Qué significa el concepto de devengo?
El devengo en el fondo es un proporcional de lo que has ganado por tener tu bono durante cierto tiempo, pese a que aún no te hayan pagado nada. Así, si nada más ocurre en la economía, luego de tener el bono por 1 año, este debería valer $10.500, es decir, habrás devengado un 5% en 1 año, y así irá avanzando de forma que cuando quede un día para que paguen el bono, valga prácticamente los $16.289 que van a pagar (de nuevo, esto en el caso en que no haya riesgo de crédito).
Hay otro factor más, que recién obviamos, pero que puede hacer que el precio de tu bono cambie.
La tasa a la que alguien puede emitir deuda depende de varios factores, y en definitiva quien define la tasa es el mercado. Estos factores son principalmente las tasas de interés de mercado, el riesgo de crédito propio de quien emite la deuda (el riesgo de que no pueda pagar) y el plazo de la deuda (o duración).
De forma muy análoga, yo puedo querer pedir plata prestada a un 1% de interés, pero si no hay ningún banco que esté dispuesto a prestarme a esa tasa, no puedo “emitir mi deuda”.
Para las empresas e instituciones que emiten deuda, funciona igual, solo que el mercado es su banco. Salen a decir “Voy a emitir deuda a través de un bono que va a pagar $1.000.000 en 5 años. ¿Quién me da más?”. Y así, dependiendo de esos factores, ciertos inversionistas estarán dispuestos a pagar más o menos por esos bonos.
Digamos que el emisor de este bono que va a pagar $ 1.000.000 es el Gobierno de Chile, y que logra vender sus bonos a $800.000. La tasa implícita en ese bono es de 4,56% anual (es lo que tiene que acumular en intereses para llegar al $1.000.000 que pagará).
Un pequeño paréntesis: la deuda (bonos) que emite un gobierno en su propia moneda prácticamente no tiene riesgo de crédito, ya que el gobierno tiene la capacidad de imprimir plata para pagarte en caso de necesitarla.
Ya dijimos que el precio de ese bono irá cambiando día a día por el devengo que vaya generando (te vas acercando a la fecha de pago). El otro factor importante se llama ganancia de capital, y es un poco más complejo.
En nuestro ejemplo, dijimos que el mercado era quien le ponía precio al bono, y que para eso consideraba varios factores.
Hay bonos que suelen ser muy líquidos: transan constantemente en el mercado, se pueden comprar y vender, y por lo tanto el mismo mercado está constantemente analizando esos mismos factores que lo llevaron a valorar el bono a determinado precio.
Digamos que por alguna razón el mercado evalúa que las tasas de interés para el Gobierno de Chile deberían ser más bajas que ese 4,56% anual, porque por alguna razón se espera una menor tasa de política monetaria.
En tal caso, el bono que tú tienes, es más valioso, porque los nuevos bonos que el gobierno va a emitir probablemente pagarán tasas más bajas, pero tu ya tienes en la mano un bono que paga más que eso. Y como la tasa “de equilibrio” ahora es de un 4%, tú podrías vender tu bono a un precio que haga que el pago en 5 años vaya a ser justamente de eso, que sería a $821.927 (si devengas un 4% anual durante 5 años sobre ese monto, llegas a $1.000.000). Y con eso, ganaste $21.927 solo por movimientos en las expectativas de tasas de interés: tuviste ganancias de capital.
$$ Precio \ bono = \frac{Cupón 1}{1 + r} + \frac{Cupón 2}{(1 + r)^2} + … + \frac{Cupón N}{(1 + r)^N} = \sum_{1}^{N} \frac{Cupón_i}{(1 + r)^i}$$
Esta es la fórmula para calcular el precio de un bono: donde \( r \) es la tasa de interés de descuento para el período de pago de cupones, y \( N \) es la cantidad de períodos faltantes para el último pago del bono. En el caso de un bono cero-cupón (que paga todo al final del período), queda simplemente así:
$$Precio \ bono \ cero \ cupón = \frac{Cupón}{(1 + r)^N}$$
Como dato, una aproximación súper simple y que se ocupa mucho en finanzas para estimar la ganancia de capital de un bono por movimiento de tasas es en porcentaje:
$$Ganancia \ de \ capital = \Delta tasa \cdot plazo$$
Donde el plazo es lo que tarda el bono en pagar la inversión inicial.
En el caso anterior, las tasas se movieron 56 puntos base, y la duración es de 5 años, por lo que la ganancia de capital debió ser de 280 puntos base, o 2,8%. El 2,8% de $800.000 es $22.400, muy parecido a los $21.927 que calculamos antes.
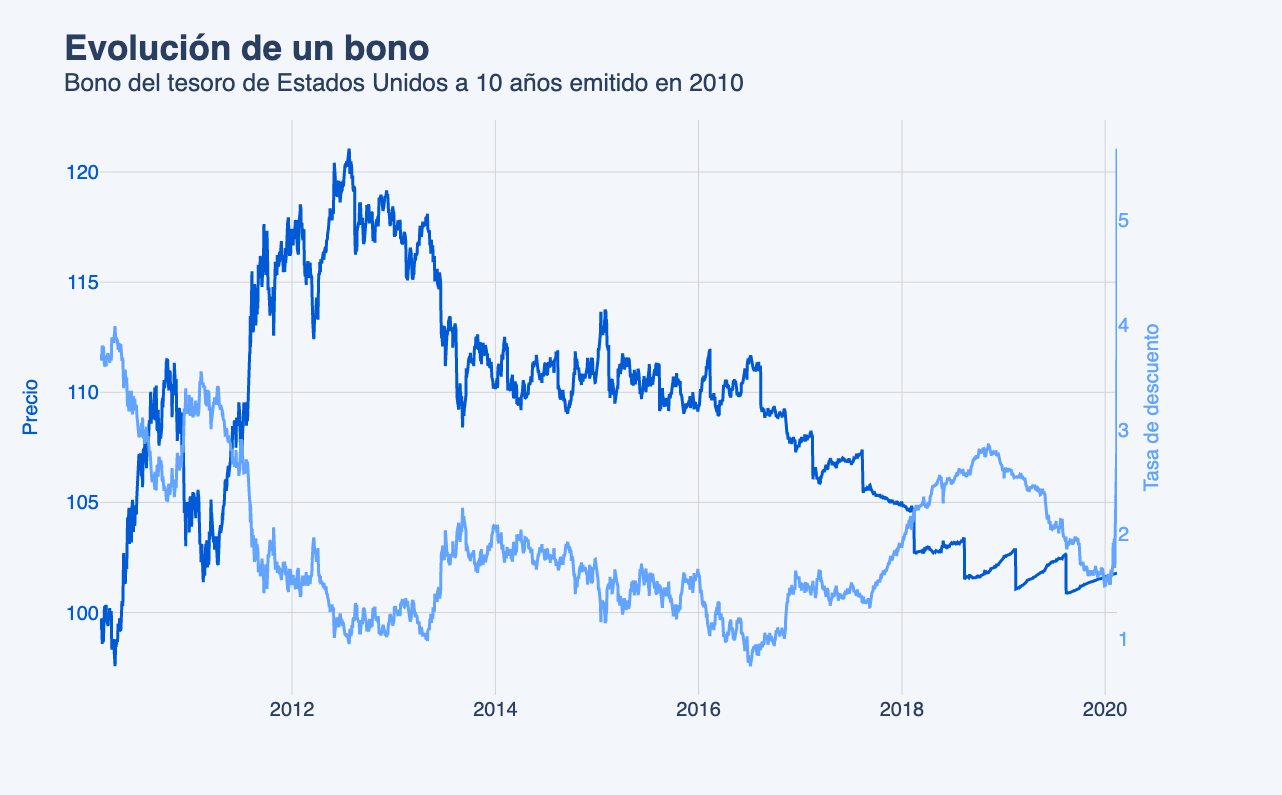
En el gráfico anterior se puede observar la evolución del precio de un bono, junto a su tasa de descuento. Se puede ver que los movimientos de tasas al principio del período influyen fuertemente en el precio, es decir, generan grandes ganancias (o pérdidas) de capital, y a medida que se va acercando al vencimiento, su sensibilidad a las tasas es cada vez menor. Los saltos discretos que se ven en el precio son producto del pago de cupones.
Como anécdota, y para reforzar este punto de cómo disminuye la sensibilidad a las tasas acercándose al vencimiento, se puede notar que justo al final del período, la tasa de descuento tiene un salto muy grande: el inicio de la pandemia, que disparó las tasas de interés, pero que prácticamente no tuvo influencia en el precio de este bono.
Como ves, tanto los devengos como las ganancias de capital harán que el precio de tu bono vaya fluctuando en el tiempo, pero es importante tener presente que no cambiarán los montos que recibirás por conceptos de cupones por tener el bono, por lo que, si lo mantienes hasta el final de su plazo, no importarán ni los devengos ni las ganancias de capital, y de ahí que recibirás una renta fija.