Ayer vi en Twitter/X que los números de votos de la elección reciente en Venezuela fueron los siguientes (los porcentajes con distintas precisiones de decimales en el redondeo son hechos por mí):
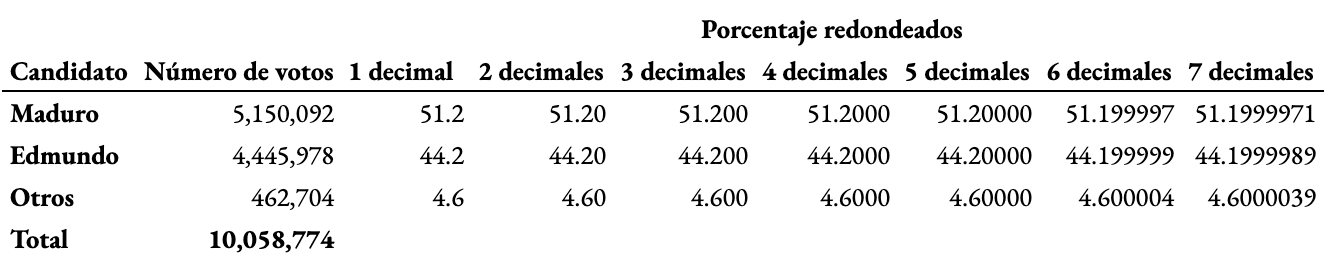
Si notan, redondeando hasta el decimal 5 el porcentaje de votación, el redondeo da con varios ceros: 4 ceros. (Desde el redondeo con 6 decimales en adelante ya no).
Extraordinario esto, según anunció la CNE la noche de la elección, los resultados fueron:
— Leo Tornarolli (@ltornarolli) July 30, 2024
Maduro 51.2%
Edmundo 44.2%
Otros 4.6%
Pero si queremos saber % con varios decimales, y recurrimos a número de votos, vemos que no hubo ni un voto de desvío de números redondos: https://t.co/9E1qJRLrBq pic.twitter.com/KKBDkUBeK0
Una pregunta natural de algún curioso sería: ¿qué tan probable es que redondeando con 5 decimales den 4 ceros a la derecha a dos candidatos al mismo tiempo?
Vamos a los números.
Notemos que en la tabla informaron que votaron 10,058,774 personas, así que vamos a asumir qué tan probable es lo que pasó dado ese número de votos (el problema asumiendo una distribución probabilística de números de votos es más extenso de analizar, pero la conclusión es la misma en todo caso).
Ahora, ¿cómo se podrían haber comportado todos esos votos? Curioso desafío matemático: necesitas dividir el número 10,058,774 en tres números naturales. ¿Cuántas combinaciones posibles se pueden formar?
La respuesta es la siguiente: si ningún número natural es cero, entonces es equivalente a resolver el problema "cuántas formas de etiquetados puedo elegir para los dos primeros candidatos desde un total de 10,058,774 - 1 etiquetas", ya que de esa forma puedo crear una distribución de los 10,058,774 votos entre 3 "cajitas" (para eso, ordeno los votantes de 1 a 10,058,774 y "corto" los grupos según las dos etiquetas).
El problema de arriba es un problema combinatorial conocido: hay
$$\binom{10,058,773}{2} = \frac{10,058,773!}{2! \cdot (10,058,773 - 2)!} = 50,589,452,103,378$$
combinaciones posibles de que se distribuyan votos para tres grupos de candidatos. Un número astronómico.
Entonces, tenemos muchas combinaciones, pero ¿cuáles de esas satisfacen que al redondear a 5 decimales su porcentaje, los 4 últimos sean ceros consecutivos? Es decir, ¿cuáles números de 1 a 10,058,773 satisfacen que, al dividir por 10,058,774 y multiplicar por 100, y luego redondear a 5 decimales, los 4 últimos decimales (a la derecha) son ceros consecutivos?
Esto se puede resolver con un pequeño script en Python*. El programita encontró 1005 números que cumplen tal condición, incluido 5,150,092 y 4,445,978. Acá dejo todos los números:
(Notar que este problema tiene la misma solución si uno asume a priori si un candidato tendrá o no "un orden de x% de votación", por lo tanto, las creencias a priori de órdenes de magnitud de votación de cada candidato no aportan información a la solución.)
Entonces, tengo 50,589,452,103,378 formas de elegir dos números de votos para los primeros dos candidatos, pero solo 1005·(1005-1) = 1,009,020 formas de que esas elecciones cumplan que sus porcentajes, redondeados a 5 decimales, tengan 4 ceros a la derecha.
Eso quiere decir que lo que acabamos de ver es un evento de probabilidad 1,009,020/50,589,452,103,378. En simple, es prácticamente un evento de 1 en 50 millones, o con probabilidad de aproximadamente 0.000002%.
Por el momento, gracias a Gonzalo Mena en Twitter/X (profesor asistente en el Departamento de Estadística y Ciencia de Datos de la Universidad Carnegie Mellon, previamente, trabajó en la Universidad de Oxford y Harvard, y obtuvo su doctorado en Estadística en Columbia University), que me mencionó ayer que una estimación inicial no estaba bien por al menos un par de órdenes de magnitud, y que hoy me pudo confirmar que está de acuerdo con el cálculo actual.
De acuerdo
— Gonzalo Mena (@mena_gonzalo) July 31, 2024
*Notas:
- Feliz si alguien encuentra que falta algo en el cálculo.
- El script de Python es el siguiente:
import csv
def check_condition(num):
result = (num / 10_058_774) * 100
rounded = round(result, 5)
return f"{rounded:.5f}".endswith('0000')
matching_numbers = []
for i in range(1, 10_058_774):
if check_condition(i):
matching_numbers.append(i)
with open('matching_numbers.csv', 'w', newline='') as csvfile:
writer = csv.writer(csvfile)
writer.writerow(['Número'])
for num in matching_numbers:
writer.writerow([num])
print(f"Se encontraron {len(matching_numbers)} números que cumplen la condición.")