El pasado importa, pero ¿cuál de todos?
El mercado financiero, siendo reflejo de la economía y la sociedad en su conjunto, es un escenario dinámico que evoluciona y varía constantemente. Un simple análisis de la historia de los mercados, considerando sus cambios tecnológicos y regulatorios, hacen evidente que ha sufrido cambios dramáticos, y que considerarlo como un fenómeno estático es un error.
Este hecho desafía a todos quienes buscamos estudiar y analizar el mercado, donde la historia pasada es la principal o única fuente de información para entender su comportamiento. Esta necesidad se exacerba con la introducción de técnicas de análisis estadístico o machine learning que requieren mayores volúmenes de datos para operar.
Dado lo anterior, los gestores necesitan usar la historia como fuente de datos para calibrar y optimizar sus portafolios, a pesar de que no toda la historia es igualmente relevante. En ese contexto, ¿cómo podemos medir la relevancia o similaridad de un periodo (histórico o sintético) con el presente?.
¿Cómo medir la similaridad?
En este artículo se revisarán 4 metodologías diferentes para entender qué es la similaridad entre escenarios económicos y cómo calcularla:
- Geometría
- Estadística
- Machine Learning
- Deep Learning
Método 1: Geometría
Lo similar = lo cercano
La similaridad es una noción muy fácil de entender porque la usamos diariamente. Desde un punto de vista matemático, es posible usar la noción de medida y distancia como aproximación de similaridad. Es decir, si puedo expresar cada escenario económico como un punto (en algún espacio), la similaridad entre dos escenarios se entiende como una función inversa de la distancia entre éstos. Por ejemplo, la similaridad puede definirse como:
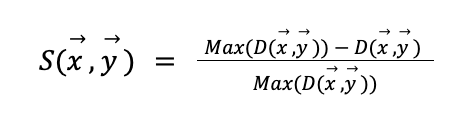
Donde \( D(x ,y ) \) es alguna definición de distancia entre dos escenarios x e y.
Distancia euclidiana
Es el tipo de distancia más común y refleja el cómo medimos distancia de forma geométrica (el largo de la recta que une ambos puntos). Formalmente se define como:
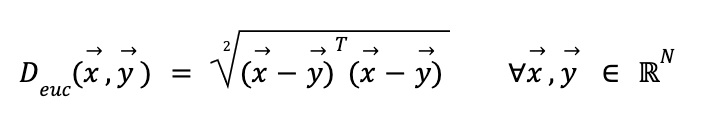
Si bien es una forma útil e intuitiva de definir distancia (y por extensión similaridad), esta medida posee varios problemas. La existencia de variables correlacionadas sobrepondera la relevancia de sus factores comunes. Por ejemplo, si elijo usar 3 variables de las cuales 2 están altamente correlacionadas, como sería la tasa de interés a 1 año y la tasa a 2 años versus el retorno de mercado, la tasa va a ser el factor preponderante en determinar similaridad por sobre los retornos, lo que puede sesgar la medición.
Método 2: Estadística
Como mencionamos antes, una de las debilidades de usar distancias meramente geométricas en el espacio original es que desconocen la dimensión estadística del problema a analizar. Las variables a medir se pueden entender como muestras de algún proceso estocástico, por lo que el considerar elementos característicos de su distribución, como sus promedios, varianzas y correlaciones ayuda a dar una intuición más acertada respecto a qué es similar y qué no.
Distancia de Mahalanobis
En vista de las limitaciones antes mencionadas, existen definiciones de distancia más afines al uso de comparar escenarios económicos. Una de ellas es la distancia de Mahalanobis, que ha demostrado poseer características útiles para el análisis financiero (Stockl & Hankle 2014, Kritzman & Yuanzhen 2010).
Creada en 1936 por el científico indio Prasanta Mahalanobis y usada inicialmente para medir y comparar cráneos humanos en estudios antropológicos, representa una generalización multidimensional al expresar distancias como el número de desviaciones estándar entre una muestra y otra. Es decir, asumiendo que cada elemento es una muestra de una distribución aleatoria Q ℝn, con una matriz de covarianza S (definida positiva), la distancia de Mahalanobis entre dos vectores x, y es:
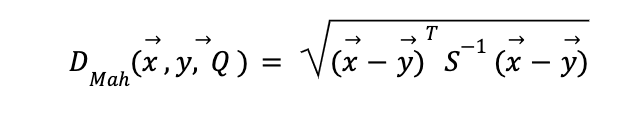
El beneficio de esta medida es que reconoce la necesidad de ajustar la topología del espacio de medición a las propiedades estadísticas de las variables a medir. De hecho, es posible demostrar empleando el teorema espectral que
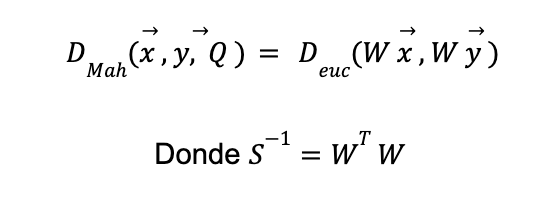
Es decir, la distancia de Mahalanobis es equivalente a calcular la distancia euclidiana después de realizar una transformación esférica del espacio original, donde W x sigue una distribución de media 0 y matriz de covarianza igual a la matriz identidad.
Metodo 3: Machine Learning
Hasta ahora, la medición de similaridad se ha mantenido circunscrita al supuesto que la relación entre las diferentes variables son lineales. Esta limitación choca con la noción de que los mercados y la economía en general son altamente no lineales, sus correlaciones varían dependiendo de los niveles del mercado, y que hay fenómenos de retroalimentación y convergencia a la media que hacen que una representación lineal de la similaridad entre escenarios sea incompleta.
Proyección a espacio latente vía TSNE
Uno de los métodos más populares para proyectar variables multidimensionales a un espacio menor de manera que se considere la no linealidad del fenómeno a medir es usar algoritmos de T-Distributed Stochastic Neighbour Embeddings, o TSNE.
Desarrollado inicialmente el 2008 por Geoffrey Hinton y Laurens van der Maaten, TSNE se ha expandido rápidamente como la solución de facto para representar set de datos altamente no lineales y multidimensionales, llegando a ser usado inclusive en genómica para mapear el ADN de células y organismos.
Sin entrar en detalles, TSNE es un algoritmo iterativo donde, mediante un proceso de optimización, se busca mapear un set de datos a un espacio de menor dimensionalidad. Se busca que las distribuciones de probabilidad de cercanía entre puntos en este espacio se asemejen lo más posible a su distribución en el espacio original.
Un punto importante es que este algoritmo genera mapeos que respetan solamente la estructura local de los datos, es decir, las relaciones de similaridad poseen validez ante sus vecinos cercanos, pero carecen de relevancia al comparar elementos lejanos. De esta manera, TSNE es una herramienta útil para determinar el grado de similaridad de elementos cercanos, pero no para entender la estructura global de los datos. Por ejemplo, es imposible determinar cuál es el escenario más distinto al presente usando este método.
Metodo 4: Deep Learning
¿Qué sucede si queremos unir lo mejor de los métodos anteriores, en otras palabras, una visión global que incorpore la no linealidad de la estructura de datos?.
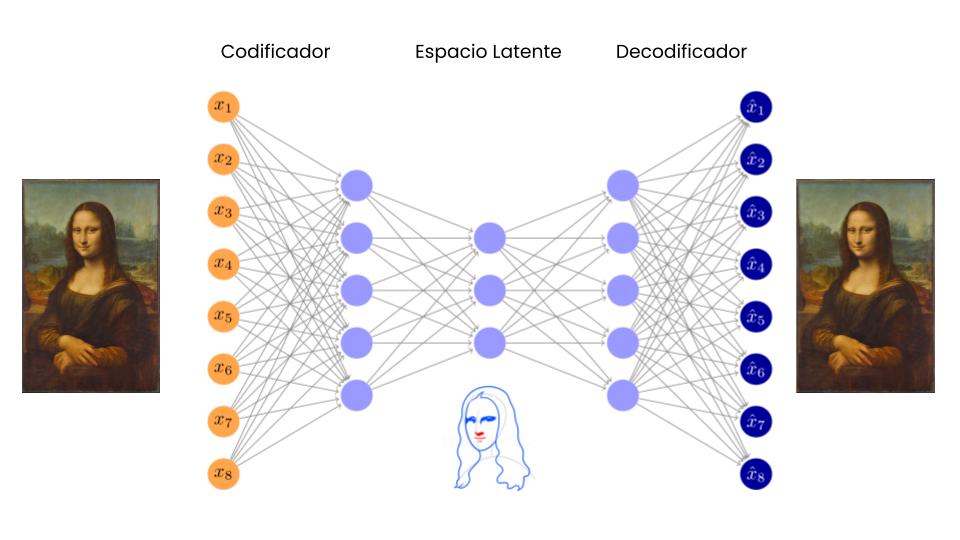
Hasta hace poco no existían modelos de estas características, pero el rápido desarrollo de modelos de Deep Learning ha generado arquitecturas de redes neuronales capaces de hacer exactamente esto: comprimir un set de datos multidimensional altamente complejo en un espacio latente coherente, que preserve toda la información y estructura relevante de los datos originales tanto a nivel local como general. Unas de estas arquitecturas son los Variational Auto Encoders o VAEs.
Proyección a espacio latente vía Variational Auto Encoders (VAEs)
La relación entre los modelos de Deep Learning y la compresión de datos es muy estrecha. La teoría del Information Bottleneck (algo así como “Cuello de botella de información”), muestra que el aprendizaje de una red neuronal profunda se sustenta en la capacidad de “comprimir” la información relevante de un fenómeno en los parámetros de la red, olvidando aquellos elementos superfluos. En esta línea, los Auto Encoders son una expresión explícita de este fenómeno, un embudo de información con el objetivo de comprimir y descomprimir información con la menor pérdida de fidelidad.
Si bien el espacio latente que existe en un Autoencoder es capaz de resumir la información relevante de cada entrada, este espacio no es necesariamente coherente, es decir, no cumple con 2 propiedades necesarias para poder medir distancia: continuidad y completitud.
La continuidad se refiere a que dos puntos cercanos en el espacio latente debieran, una vez decodificados, producir resultados similares en el espacio real. Mientras que la completitud refiere a que cada punto en el espacio latente (sujeto a alguna distribución) debiese generar resultados coherentes una vez decodificados.
Para obtener un espacio de estas características, los VAEs expanden un Autoencoder para transformar el espacio latente en uno estocástico, donde en vez de proyectar al espacio latente directamente, un VAE cambia a una función de densidad (usualmente gaussiana) sobre este espacio, y la decodificación se realiza sobre una o varias muestra aleatorias sacadas de esta distribución. De esta manera un elemento, al ser codificado al espacio latente, toda su vecindad definida por su función de distribución debiese generar escenarios similares en el espacio final.
Planteamiento y metodología
Datos
Para estimar estos modelos y ver qué periodos del pasado se parecen al presente, vamos a emplear un set de 3 tipos diferentes de información contextual del mercado y la economía:
- Retornos de mercado por clase de activo: probablemente la forma más directa de analizar el mercado. Los retornos de activos, sumado a sus volatilidades y correlaciones con otros activos, son un buen reflejo del mercado y sus diversos estados.
- Niveles de tasas y spreads corporativos de la renta fija norteamericana: existe consenso, tanto en la academia como en los actores de mercado, de que la curva de tasas refleja los elementos relevantes de la expectativa macroeconómica (y en extensión del mercado). Por ejemplo una inversión en la curva refleja una visión contractiva de la economía, mientras que su empinamiento apunta a su aceleración y/o sobrecalentamiento.
- Inflación y ciclo industrial: las definiciones más básicas de ciclos de mercados se relacionan al ciclo de crecimiento/inflación presente en la economía. En este caso empleamos inflación e índice de optimismo industrial (PMI) a nivel de Estados Unidos (como principal driver de retornos en los mercados globales) y los valores agregados a nivel mundial.
Se emplearán las series mensuales desde 1990 de todos los indicadores para el estudio. Sería deseable realizar un análisis más extenso, pero inevitablemente el universo de índices a disposición con semejante historia se reduce dramáticamente.
Resultados
Proyecciones en espacios latentes
El primer resultado que vale discutir es cómo las diferentes técnicas de mapeo a espacios latentes difieren. En línea con la intuición de los modelos, TSNE busca proyecciones concentradas en grupos de alta similaridad (usualmente periodos continuos de tiempo donde el mercado/economía se mantuvo en un estado muy similar). En este sentido, el presente además de parecerse al pasado inmediato, guarda similaridad con periodos como el 2008.
Por el contrario, el Variational Autoencoder hace una proyección mucho más homogénea en el espacio latente de los diferentes periodos, permitiendo entender una “historia más completa”, donde si bien hay una dimensión relativamente monotónica con la antigüedad del escenario (más antiguo a la derecha, más reciente a la izquierda), ese cambio se reversa en los últimos periodos, donde fines del 2022 se aleja del pasado reciente y se aproxima a periodos tipo 2008 y anteriores.
También es importante recalcar que para que los VAEs sean una metodología estable, es necesario ajustar sus hiperparámetros de manera de conseguir convergencia en la red. Para el caso particular del dataset analizado, la arquitectura empleada fue relativamente simple (4 capas con dimensionalidad de 14, 7, 7, 14), learning rate de 0.0001 y 10.000 epochs con un batch size de 500 elementos por iteración.
Estimación de similaridad
Para cada metodología computamos la similaridad promedio de cada periodo contra los últimos tres periodos de análisis (octubre, noviembre y diciembre 2022). Los resultados son los siguientes:
Conclusiones
Comparando las 4 medidas podemos hacer las siguientes observaciones:
Si bien tanto la distancia Euclidiana como de Mahalanobis sobre el espacio original tienden a dar mayor similaridad a periodos más recientes y descartar periodos pasados como relevantes, las proyecciones vía TSNE y VAE dicen lo contrario. Esto es relevante ya que significa que al considerar los efectos no lineales de las relaciones entre crecimiento, tasas y retornos, el periodo actual dista fuertemente del pasado reciente, forzándonos a volver la mirada hacia periodos anteriores. Esta señal coincide con la intuición de que el régimen de mercado de baja inflación y bajas tasas, que dominó transversalmente al mercado durante la última década, ha sufrido cambios estructurales que lo asimilan más a los períodos pasados de inflaciones y tasas mayores.
Existe una coincidencia transversal en la similaridad entre el periodo actual al 2008-2009 (crisis sub-prime) pero una coincidencia más leve al periodo 2011 (crisis europea) y existe consenso respecto al periodo 2000 (crisis punto-com). Esto apunta a algo simple: no todas las crisis son iguales y cada una tiene que ser estudiada bajo su propio mérito. Sin embargo, de esta señal también se puede leer que existe consenso en que el periodo actual debiera estudiarse como un escenario de crisis, alejado de los periodos más normales del mercado.
Como conclusión, si bien ninguna de las técnicas antes expuestas posee necesariamente la verdad absoluta, su análisis conjunto puede aportar una visión más precisa y matizada del escenario económico actual, con el propósito de desarrollar mejores modelos de valorización, construcción de portafolios y gestión de riesgo.