En términos generales, se puede decir que hay dos tipos de problemas matemáticos: aquellos que son fáciles de resolver (existe una fórmula para encontrar la solución) y aquellos que son difíciles de resolver (no se conoce la fórmula, o es tan complicada que en la práctica no es muy útil).
Un ejemplo del primer tipo es la famosa ecuación de segundo grado que todos aprendimos en la educación secundaria:
$$
Ax^2 + Bx + C = 0
$$
Conocidos los valores de A, B y C, existe una fórmula explícita para encontrar los valores de x que la satisfacen.
El desafío es que hay muchos problemas prácticos que pertenecen al segundo grupo, es decir, no hay una manera directa de resolverlos. Pero afortunadamente, existe un método indirecto, versátil y fácil de implementar, para tratar estos problemas: los métodos de Monte Carlo (también conocidos como Monte Carlos o simulaciones de Monte Carlo).
Los Monte Carlos tuvieron su origen durante la Segunda Guerra Mundial, cuando EE.UU., como parte del Manhattan Project, montó un programa para desarrollar armas nucleares. La idea del Monte Carlo es simple: generar muchos casos (escenarios es el término técnico) plausibles, en forma aleatoria, de tal manera que al examinarlos uno pueda identificar las tendencias generales del fenómeno estudiado. El fundamento matemático se basa en un resultado conocido como la Ley de los Grandes Números. Esta establece que si repetimos un experimento varias veces, en forma aleatoria, a la larga el resultado promedio se va acercando al valor correcto. Si bien los Monte Carlos nacieron en los años 40, su uso se popularizó recién durante los años 60, cuando los computadores se empezaron a incorporar a las universidades, centros de investigación y grandes empresas. El nombre Monte Carlo se debe al famoso casino en la Costa Azul. Lo sugirió un matemático del Manhattan Project, que vio la conexión probabilística entre ambos, es decir, los juegos de azar y el método de simulación.
Consideremos la siguiente situación: el operador de un centro de esquí necesita estimar la cantidad de nieve para la próxima temporada. Para esto, genera 10.000 escenarios posibles de nevadas usando un modelo basado en datos históricos ajustados por tendencias climáticas recientes. Y analizando las tendencias mostradas por estos escenarios, puede determinar si la temporada será buena, regular o mala, y así hacer una proyección de ingresos.
¿Qué pasa si ahora queremos hacer un cálculo más refinado e incorporar la temperatura? Después de todo, la temperatura influye en cuánto dura la nieve sin derretirse. Evidentemente, el Monte Carlo debe ahora considerar dos variables, nieve y temperatura. Esto introduce un nivel adicional de complejidad: la necesidad de incorporar la interdependencia entre ambas variables. Evidentemente, lo más fácil sería suponer que ambas son independientes, y modelarlas en forma separada. Pero esta no es una buena idea ya que terminaríamos generando unos escenarios imposibles: por ejemplo, combinaciones de altas temperaturas con nevazones. ¿Cómo describir entonces la interdependencia entre la nieve y la temperatura?
La alternativa más simple es apoyarse en la correlación, un concepto formalizado por Karl Pearson a fines del siglo diecinueve. En términos intuitivos, la correlación (que puede tomar valores entre -1 y 1) refleja el grado en que dos variables se mueven al mismo tiempo. Valores positivos se refieren a variables que tienden a aumentar y disminuir más o menos al mismo tiempo. Por ejemplo, en los seres humanos, el peso y la altura, o el nivel de ingresos y años de escolaridad. Por el contrario, existe una correlación negativa entre la expectativa de vida y el número de años que una persona ha fumado.
Si suponemos que la temperatura y el nivel de nieve acumulada en un periodo siguen una distribución normal, una manera de modelar en forma simultánea estas dos variables es usando una distribución normal multivariada. En el fondo, una distribución normal en dos dimensiones, donde la interdependencia entre nieve y temperatura se describe a través de la correlación. Si bien esta alternativa representa un avance en comparación con la suposición de independencia, tiene algunas limitaciones. La evidencia empírica indica que la nieve y la temperatura siguen patrones que se apartan un poco de la distribución normal. Y la correlación solo captura bien interdependencias lineales.
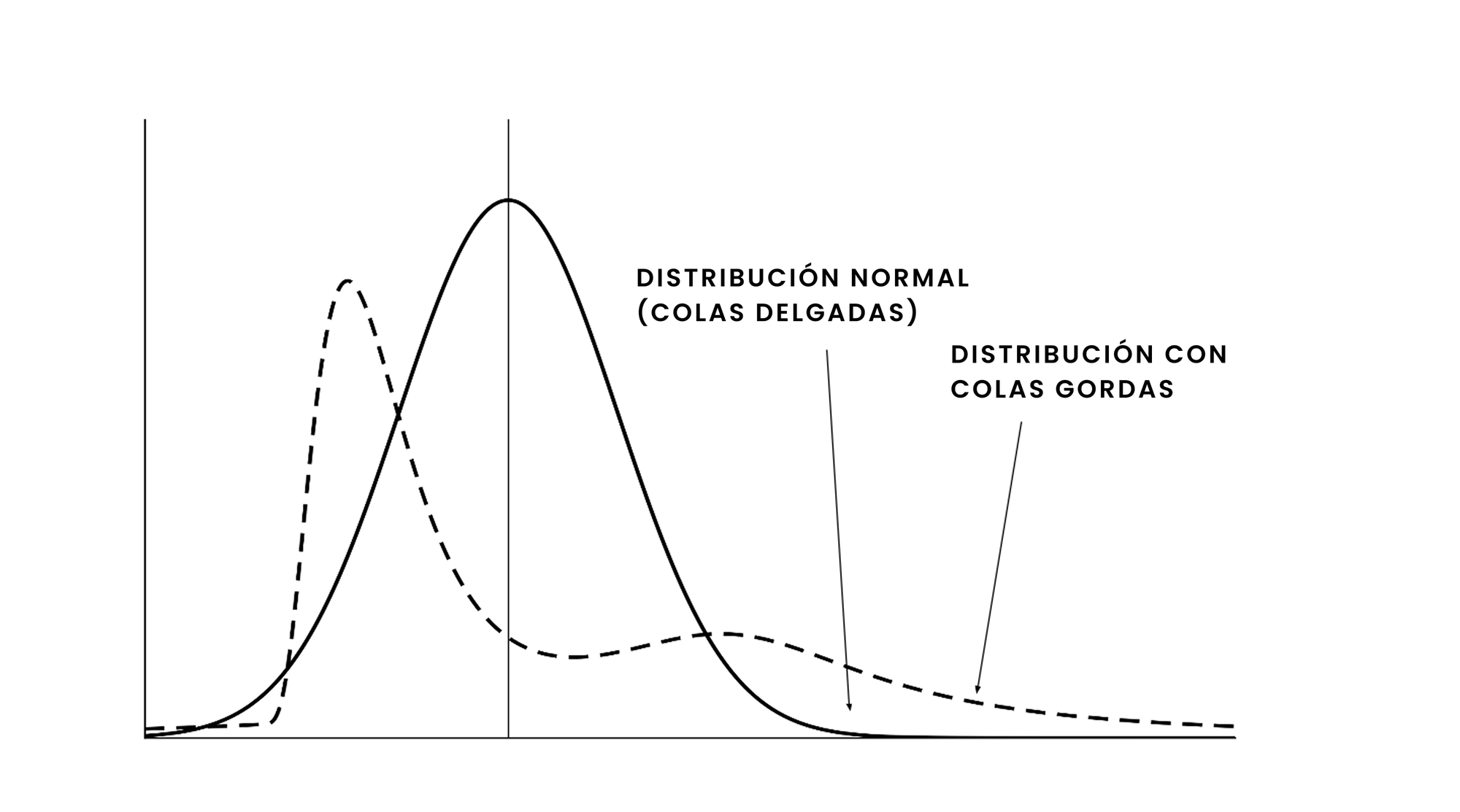
Desafortunadamente, más allá de la nieve y la temperatura, existen muchas otras variables en el mundo real que no siguen una distribución normal y cuyas interdependencias son más complejas que lo que se puede describir con un simple coeficiente de correlación lineal. En el ámbito de las finanzas, es sabido que los retornos de activos financieros siguen distribuciones marcadamente diferentes a la curva normal: son asimétricos y presentan "colas gordas" (la curva normal es simétrica y sus colas son "delgadas").
Por otro lado, un caso típico de interdependencia no-lineal es la que existe entre la edad y el ingreso. En general, esta relación se asemeja a una parábola invertida: cuando la persona es joven, el ingreso tiende a aumentar con la edad; y a partir de un cierto punto, el ingreso tiende a disminuir a medida que la persona envejece. Este tipo de interdependencia (en términos matemáticos, una relación cuadrática), no es susceptible de describirse a través de un coeficiente de correlación lineal. De hecho, en este caso la correlación es cercana a cero, lo que sugeriría (erróneamente por supuesto) que no hay ninguna relación entre edad e ingreso.
Lo concreto es que hasta mediados de los años 90 la mayoría de los Monte Carlos con varias variables se basaban en la correlación para modelar la interdependencia, y por ende, en la normal multivariada. Desgraciadamente, en muchos casos prácticos, específicamente cuando lo que interesa es estimar la probabilidad de eventos extremos, es donde más severamente se manifiestan las limitaciones de esta decisión. Ejemplos abundan: en hidrología, la descarga fluvial (de un río específico) y la lluvia siguen ambas distribuciones asimétricas y de colas "gordas" y su interdependencia no es lineal; lo mismo sucede en la ingeniería costera, donde la interdependencia entre la altura de las olas y el periodo (tiempo entre ellas) es no-lineal, y ambas variables siguen distribuciones diferentes a la normal. En todos estos casos, un Monte Carlo hecho con las suposiciones descritas tiende a subestimar la probabilidad de eventos extremos, que justamente son los más relevantes en un contexto de análisis de riesgo.
¿Cómo hacer entonces para modelar en forma más real (o mejor dicho, más precisa) la interdependencia entre variables cuyo comportamiento no se puede describir con la distribución normal? La solución la dio Abe Sklar en 1959.
Sklar, un matemático norteamericano de origen ucraniano y que obtuvo su doctorado en Caltech en 1956 bajo la supervisión de Tom Apostol (autor del libro de cálculo que muchos estudiantes de ingeniería y física probablemente usaron y recuerdan), viajó a Francia a hacer un post-doc después de graduarse. Y en París, bajo el auspicio del Instituto de Estadísticas de la Universidad de París, publicó en 1959 el artículo por el cual es más conocido hoy día: Fonctions de répartition à n dimensions et leurs marges (Funciones de distribución n-dimensionales y sus marginales). En este, Sklar introdujo un concepto revolucionario: las cópulas.
La idea brillante de Sklar fue separar los dos aspectos fundamentales del problema: las características individuales de cada variable (que pueden tener cualquier distribución, no necesariamente normal) y la estructura de interdependencia entre ellas (que puede ir más allá de la simple correlación lineal). Para lograr esto, desarrolló una clase de funciones que denominó cópulas, y abrió un universo impensado de posibilidades ya que liberó a las simulaciones Monte Carlo del yugo impuesto por las distribuciones normales multivariadas y sus limitaciones. En el fondo, las cópulas capturan lo que se puede describir con un coeficiente de correlación lineal más una gran cantidad de opciones adicionales.
La siguiente analogía permite ilustrar la idea básica. Supongamos que dos tenistas con estilos completamente diferentes deciden formar una dupla para jugar dobles. El primero se destaca por su saque potente y su juego de fondo; el segundo, por su agresividad en la red y poseer un servicio más débil. Lo que hacen las cópulas—en sentido figurado—es modelar la dinámica de cómo estos jugadores interactúan y se complementan en la cancha, sin necesidad de modificar las características individuales del juego de cada uno. En síntesis, las cópulas permiten a los Monte Carlos reflejar no solo las peculiaridades de cada variable, sino también la verdadera naturaleza de sus interdependencias.
Las primeras aplicaciones de las cópulas fueron en los años 90. En ciencias actuariales, se usaron para crear tablas de mortalidad conjunta (entre cónyuges o parejas estables), y en hidrología, para modelar la dependencia, durante inundaciones, entre el volumen total de agua descargado y el flujo (instantáneo) máximo. Y a partir de los años 2000, la ingeniería financiera adoptó en forma generalizada las cópulas como la técnica preferida para modelar dependencias, siendo el caso más común, la relación entre los retornos de distintos activos financieros. Hoy día el uso de cópulas, en combinación con Monte Carlos, es habitual en problemas de meteorología, geotecnia, control de calidad, riesgo operacional, epidemiología, ciencia de los materiales, y gestión energética, entre otros.
Curiosamente, la economía—al contrario de las finanzas y la ingeniería financiera—ha demorado bastante en descubrir los beneficios de las cópulas, y aún hoy día, su aplicación no ha alcanzado el nivel de popularidad visto en otras disciplinas. De hecho, la economía todavía permanece excesivamente aferrada a la econometría y las regresiones lineales.
El lector astuto habrá notado que pasaron casi cuarenta años entre la publicación del artículo de Sklar (1959), y las primeras aplicaciones de las cópulas a problemas prácticos (mediados de los años 90). ¿A qué se debió este retraso?
La respuesta es simple y al mismo tiempo sorprendente: Sklar publicó su artículo en francés. Y el mundo angloparlante (excesivamente autorreferente, pero hay que admitirlo, el único relevante en términos científicos y técnicos) se demoró en leerlo y apreciar su potencial. El caso de Sklar, sin embargo, no es único. Algo similar ocurrió con Bachelier y su tesis de doctorado: Théorie de la spéculation. Este trabajo, publicado en 1900 por la Universidad de París, estableció los fundamentos de lo que hoy se conoce como matemáticas financieras, si bien permaneció ignorado hasta que Paul Samuelson lo popularizó en los años 50. Los avances de Kiyosi Ito en procesos estocásticos (el lema de Ito juega un rol importante en la derivación de la ecuación de Black-Scholes) demoró menos en ser reconocido internacionalmente. El artículo original (en japonés) es del año 1942 y la traducción al Inglés es de 1951.
Surge entonces la pregunta: ¿habrá en estos momentos otros trabajos importantes ignorados simplemente por haber sido publicados en el idioma "equivocado"? ¿Algún teorema matemático que se haya divulgado en árabe, mandarín o bengalí y que esté esperando ser "descubierto" por el resto del mundo? Tendremos que esperar algunos años para saberlo. Pero una cosa sí está clara: existe una alta correlación entre el idioma en que se publica un resultado y la rapidez con que se internacionaliza. Y aquí sí basta con hablar de correlación, no es necesario invocar a las cópulas de Sklar. Por último, ¿cuánto tardará este artículo en traducirse al Inglés? (Bueno, no es que sea muy importante, pero para ser franco no tengo ninguna esperanza... ja, ja, ja.)